教室ブログ

「たとえ、世界中の人が《わかった、簡単だよ》と言ったとしても、自分がわかっていなかったら《いや、自分はわかっていない》と言う勇気。それが大切なんだ」ー『数学ガール／ゲーデルの不完全性定理』第5章より

最近ちょっと感動した言葉を記してみました。

--------

「わかる」ためには、まず「わかっていない」ことを自覚できることが大切です。

でも、集団教育の中では、それには多少の勇気が要ります。

「みんなと同じ」状態は安心であり、

「みんなと違う」状態は怖いから。

これはほとんど本能でしょう。

だからこそ、家庭や私塾など、個別教育が可能な場では、あえて「みんなと同じでなくていい」と教えることが必要ではないかと思います。

わかならくても怒られない

わからないときはいつでも訊ける

わかるまで待ってもらえる

そんな安心感をまずは与えてやりたいと思います。

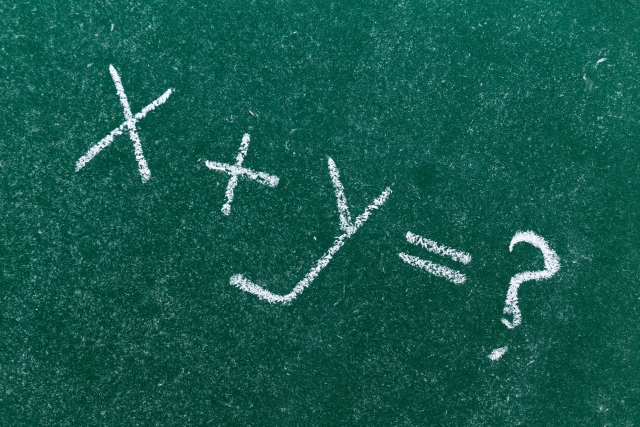
数学の話題です。

学習指導をする中で、生徒の躓(つまづ)きから学ぶことが多々あります。

今回はその1つについてお伝えしたいと思います。

今、中一生は学校で「正の数・負の数」を学習中と思いますが、

その加法・減法の計算に躓いていませんか？

もしそうなら、次の式中の「＋」をどう読むか調べてみて下さい。

＋5＋＋3　(カッコはあえてつけていません)

正しい読み方は「プラス5　たす　プラス3」です。

もし、下のいずれかに当てはまるとしたら、早目に手を打つ必要があります。

①「＋5」を「たす5」と読む

②「5＋＋3」を「5たすたす3」または「5プラスプラス3」と読む

①のような読み方をする場合は、

正の数・負の数とは何か、がわかっていない可能性があります。

②のような読み方をする場合は

「計算記号の＋－(たす・ひく)」と「符号の＋－(プラス・マイナス)」を区別できていない可能性があります。

この区別については、教科書では触れられておらず、指導上の盲点となりやすい箇所です。

詳しく見てみます。

「計算記号の＋－」は、

前後の2つの数について「たす・ひく」という動作をする、の意味を持ちます。

英語でいうと「動詞」の働きを持ちます。

それに対して、「符号の＋－」は、

「正の数か、負の数か」の区別を表します。

英語でいうと「冠詞」(aやthe)の働きします。

両者は同じ記号を使いながら、意味や働きが全く異なりますので、

学習の初期においては、躓きの原因になりやすいのです。

この区別は「項」の理解に欠かせない根本的な事柄ですし、今後の方程式の解法にも関わります。

もし現時点で躓いているのなら、しっかり区別するよう指導をしたいところです。

5/15のブログで、こんな問いを立ててみました。

＜「無限」という語彙を持つことと、算数・数学ができることとの間には、どんな関係があるのか ＞

考えても結論が出ないので、ネットで調べてみたところ、

次のような研究が目に留まりました。

●福島大学付属図書館

子どもにおける連続と無限多概念の発達について

研究によると、子どもはいきなり「無限」について理解するのではなく、

まずは「稠密性」の概念を獲得し、

その後「連続性」や「無限多」の概念へと進むようです。

数の稠密性や連続性は、量や関数の理解に欠かせない概念ですから、

それらの概念が獲得されていないと、上記単元で躓くことが容易に予想されます。

したがって、「無限」をボキャブラリーとして持っている子は、稠密性や連続性については当然クリアーできており、

量や関数については十分理解可能、すなわち算数・数学ができることが多いのであろうと思われます。

小６の算数に「対称な図形」という単元があります。

その中で「線対称」「対称の軸」について、毎年、次のような問答をしています。

私「正方形には、対称の軸が何本ある？」

生徒Ａ「２本」

私「もっとあるぞ」

生徒Ａ「…あー、４本」

私「正六角形には？」

生徒Ａ「…6本」

私「正八角形には？」

生徒Ａ「…8本」

私「では、円には？」

この問いに対する生徒の答え方は、だいたい次の４通りに分かれます

● たくさん

● わからない

● 数え切れない

● 無限

どの答え方も、同じ事柄を言おうとはしているようです。

しかし、とりわけ「無限」と答えられる生徒は、算数・数学がよくできる傾向があると、最近気がつきました。

傾向が見えると、それはなぜなのか知りたくなります。

そこで次のような問いを立ててみます。

＜「無限」という語彙を持つことと、算数・数学ができることとの間には、どんな関係があるのか ＞

もしその関係が分かれば、算数・数学を得意にする、1つの方略が見えてくると思われます。

（いつかに続く）

小学生の頃の話。近所のお肉屋さんにお使いに行ったことがあります。

店の左右の壁際には、鏡が１枚ずつ据えつけられていました。

左に目を遣ると、自分の姿が写っています。

右に目を遣ると、やはり自分の姿が写っています。

「！！！」

すごい発見をしました。

鏡の中に鏡がある。その鏡の中にも鏡がある。その鏡の中にもまた鏡が！

いったいどこまで続いていくのだろう

それを見極めようと、顔を近づけてみました。

鏡の中の自分は、表、裏、表、裏しながら、どこまでも小さくなっていきます…

（続く）

そんなことを２、３日繰り返した後、分かったのは、

「やっぱり、折り紙は伸びていない」

「たてが短くなったんだ！」

という、大人にとっては「当たり前」な、

しかし、子供の私にとっては「大発見！」なことでした。

--------

ホームページの閲覧数もまったく伸びていない…

何とかしなければ！

（教室だより作成のため、ブログはしばらくお休みいたします）

まだ小学校に上がる前だったでしょうか。

折り紙を折っていて、不思議な気持ちになったことがあります。

正方形の折り紙を半分に折って、長方形にした途端、

「びろん」と横に伸びたように感じたのです。

紙ですから、引っ張っても伸びはしません。

でも、折った瞬間、横に伸びる。

おかしいな、おかしいな、と思いながら、

何度も折ったり、広げたりしていました。

（続く）

過去の教室だよりから。(平成17年4月号)

------------------------

桜はもうすっかり見頃を過ぎてしまいました。…先日、桜が満開だった日に、大叔父からこんな話を聞きました。

小学校に上がった昭和の初め、最初の算数授業で、担任の先生は子供たちを校庭の桜の木の下に集めたそうです。

そして一枚の桜の花びらを拾い上げ、松葉に刺して言いました。

「花びらが一枚」

皆も同じように一枚拾い上げ、松葉に刺しました。

続いて先生はもう一枚刺して言います。

「花びらが二枚」

そうやって、一から十まで教えてもらった、と。

ああ、そんな教え方もいいものだなあ。

過ぎ去った遠い過去の話ですが、

桜の花びらでできた髪飾りを手に、はしゃぐ子供たちの姿が目に見えるようでした。

------------------------

改めて祖母に捧げます。

よい話をありがとう。